
Introduction
Qu’est-ce qui pourrait bien relier Peter, grutier de 34 ans en banlieue parisienne, et Chris, professionnelle de la petite enfance de 56 ans à Reims ?
Chez Maglia, leurs trajectoires se croisent autour de l’un des sujets de recherche les plus complexes : l’affectation et la planification de tâches dans un environnement multi-compétences.
Peter comme Chris sont des professionnels qualifiés, avec des compétences uniques — et cette situation se retrouve dans quasiment toutes les entreprises et institutions. Toute personne en charge de la planification doit jongler avec ces contraintes de compétences. Mais très vite, d’autres questions apparaissent :
- Quels autres critères comptent lorsqu’on assigne une personne à une tâche ?
- Comment prendre en compte d’autres objectifs comme l’équité, l’efficacité, le coût ou la satisfaction des employés ?
- Comment les mathématiques avancées peuvent-elles nous aider à relever ce défi ?
- L’intelligence artificielle peut-elle réellement s’adapter aux affectations du monde réel ?
Au fond, tout se résume à une question très humaine.
Pour Peter, cela peut être aussi simple que : « À quelle heure je commence lundi ? »
Modélisation mathématique
Considérons un ensemble de tâches $t∈T_t$, chacune définie par :
- son heure de début $s_t$,
- son heure de fin $e_t$,
- son ensemble de compétences requises $S_t$,
- son nombre d’employés nécessaires $r_t \in \mathbb{Z}_{\ge 0}$.
De l’autre côté, nous avons les employés $e \in E$, chacun caractérisé par :
- leur ensemble de compétences $S_e$,
- leur disponibilité $U_e$.
La décision d’affectation est représentée par une matrice binaire $A$, où :
\(
a_{e,t} \in \{0,1\} =
\begin{cases}
1 & \text{si l'employé $e$ est affecté à la tâche $t$,} \\
0 & \text{sinon.}
\end{cases}
\)
Comme certaines tâches peuvent nécessiter plusieurs employés, nous définissons un vecteur $Y$:
\(
y_t =
\begin{cases}
1 & \text{si la tâche $t$ est entièrement pourvue,} \\
0 & \text{sinon.}
\end{cases}
\)
Après avoir défini les variables d’affectation, nous devons garantir que le système respecte certaines règles opérationnelles essentielles. Par exemple, une tâche ne doit pas recevoir plus d’employés que nécessaire :
\[
\sum_{k\in R^q} x_{jk} \le r^{\mathrm{req}}_j.
\]
Ou encore, dans certains contextes (par exemple pour opérer une grue comme Peter), une tâche n’a de sens que si elle est entièrement pourvue des travailleurs qualifiés requis. Dans ce cas, nous imposons :
\[
\sum_{k} x_{jk} = r^{\mathrm{req}}_j\,y_j
\]
Approches de résolution du problème
La résolution de l’affectation de ressources devient alors un problème d’optimisation discrète.
L’objectif est de choisir des valeurs pour $A$ (et donc pour $Y$) de manière à ce que :
- toutes les tâches soient couvertes,
- les contraintes des employés soient respectées,
- des objectifs plus larges, comme l’efficacité, l’équité ou la minimisation des coûts soient atteints.
En pratique, cela signifie que la question de Peter n’est pas résolue « au doigt mouillé », mais bien grâce aux mathématiques.
Par exemple, l’absence de chevauchement dans les affectations peut être exprimée ainsi : $ \forall e_1, e_2 \in E, \forall t \in T, a_{e_1,t} + a_{e_2,t} \le 1$.
Des outils open source tels que le solveur CP-SAT de Google OR-Tools peuvent être utilisés pour traiter ce type de problème. Disponible en bibliothèque Python, CP-SAT est considéré comme l’état de l’art en optimisation linéaire en nombres entiers dans l’open source, et offre un moyen concret de transformer ces équations abstraites en plannings réels et opérationnels.
Réduction de la complexité grâce au pré-traitement
En pratique, la matrice complète d’affectation peut devenir extrêmement large, rendant le problème d’optimisation bien plus difficile à résoudre.
Chez Maglia, nous abordons ce défi en appliquant une étape de pré-traitement destinée à réduire l’espace de recherche aux seules affectations plausibles.
Concrètement, nous construisons une matrice réduite qui ne contient que les employés à la fois disponibles pour une tâche donnée et possédant les compétences requises.
En éliminant dès le départ les affectations impossibles ou non pertinentes, le solveur peut se concentrer sur des options réalistes, ce qui réduit drastiquement la complexité computationnelle tout en permettant d’obtenir des solutions optimales ou quasi-optimales.
Définition des objectifs et arbitrages
Chaque entreprise ou institution peut avoir ses propres objectifs de planification.
C’est pourquoi, chez Maglia, nous adaptons nos algorithmes aux priorités spécifiques de chaque client.
L’objectif le plus courant consiste à maximiser le nombre de tâches entièrement pourvues, ce qui se traduit mathématiquement par :
\[
\sum_{j\in V} d_j\,y_j,
\]
où $y_j = 1$ si la tâche $j$ est entièrement affectée.
Un autre objectif fréquent consiste à maximiser le nombre total d’heures programmées, soit :
\[
\sum_{j\in V}\sum_{k\in R^q} d_j\,x_{jk}.
\]
Dans certains cas, la direction peut attribuer des priorités différentes aux tâches en les pondérant selon leur importance.
Cela conduit à un objectif de la forme :
\[
\sum_{j\in V} w_j\,d_j\,y_j.
\]
Objectifs d'équité : Posons $h_k = \sum_j d_j\,x_{jk}$ représentant la charge de travail de l’employé $k$.
- Minimax load: introduire $L$ et minimiser $L$ sous la contrainte$h_k \le L$.
- Max-min fairness: introduire $m$ et maximiser $m$ sous al contrainte $h_k \ge m$.
- Variance / approximation de l'incide de Jain : minimiser $\sum_k |h_k - \bar h|$ où $\bar h$ est la charge moyenne.
La beauté des mathématiques réside dans cette flexibilité : dès lors que nous comprenons les objectifs réels du client, nous pouvons les traduire en formulations mathématiques précises, le cœur même de notre moteur de planification.
Les limites des méthodes exactes
Vient ensuite le défi du temps réel.
Déterminer quelque chose d’aussi simple que « À quelle heure Peter commence-t-il lundi ? » peut prendre plus de temps qu’on ne l’imagine. Plus on ajoute de tâches et d’employés, plus les possibilités deviennent riches… mais plus le calcul devient lourd.
Même après avoir réduit l’espace de recherche, la complexité de ces problèmes croît exponentiellement avec le nombre de tâches et d’employés.
Pour mieux illustrer ce phénomène, comparons deux approches différentes.
La figure ci-dessous montre l’évolution des temps de calcul entre :
- notre modèle exact en programmation linéaire en nombres entiers,
- l’heuristique Maglia.
Alors que l’heuristique reste extrêmement rapide, le modèle exact devient rapidement coûteux en calcul, même pour des problèmes de taille moyenne.
Cela met en lumière à quel point la complexité peut exploser dans la pratique.
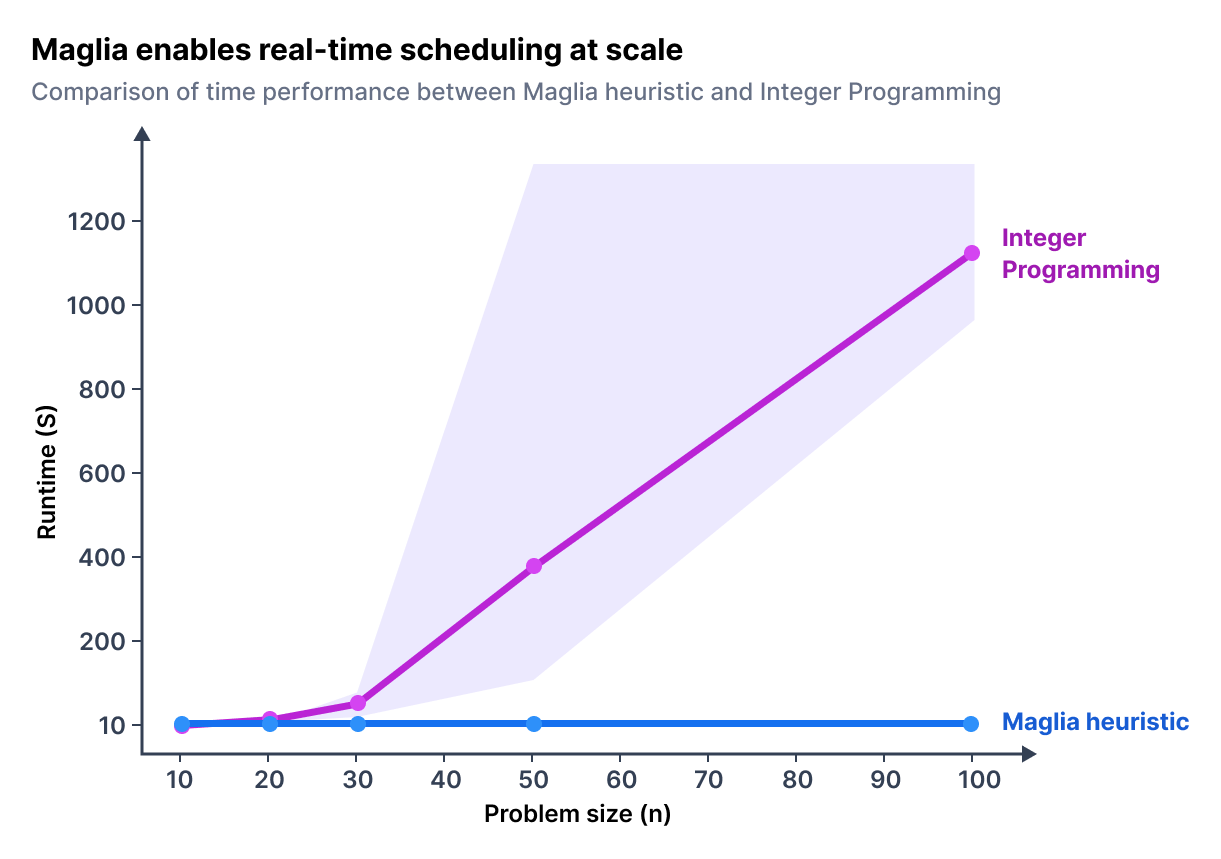
Trouver l’optimum exact : un luxe rarement compatible avec la réalité. Chercher l’optimum mathématique exact peut être extrêmement long — et pour un planificateur devant son écran, attendre plusieurs minutes voire plusieurs heures n’est tout simplement pas envisageable.
Dans la vraie vie, l’allocation des ressources doit se décider en temps réel, les plannings devant souvent être réévalués dès qu’une nouvelle information arrive.
Que se passe-t-il si un salarié devient soudainement indisponible ?
Quel impact cela a-t-il sur tout le reste du planning ?
Ces défis nécessitent des méthodes rapides et adaptatives.
Plutôt que de viser une optimalité parfaite, on peut s’appuyer sur des heuristiques intelligentes et des algorithmes guidés par l’IA capables de fournir des solutions de haute qualité en temps réel.
L’exploration de ces approches adaptatives fera l’objet d’un prochain article — et constituera l’une des fonctionnalités clés de la prochaine version du logiciel Maglia.
Références
- Demir, O., Tolga, D., & Yücel, E. — An optimization framework for a dynamic multi-skill workforce scheduling and routing problem with time windows and synchronization constraints
- Fırat, M., & Hurkens, C.A.J. (2011) — An improved MIP-based approach for a multi-skill workforce scheduling problem
- Ahmadpour, S., & Ghezavati, V. (2019) — Modeling and solving multi-skilled resource-constrained project scheduling problem with calendars in fuzzy condition
- Fırat, M., Hurkens, C.A.J., & Laugier, A. (2012) — Stable multi-skill workforce assignments
- Golab, A. — Automatisation de la planification dynamique de projet à ressource limitée par l’intelligence artificielle (Thèse de doctorat)


.jpg)